Last updated: 2024-12-06

Checks: 7 0

Knit directory: online_tut/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20241120)

The command set.seed(20241120) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: f71507f

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version f71507f. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store
    Ignored:    analysis/.Rhistory
    Ignored:    code/.DS_Store

Untracked files:
    Untracked:  analysis/_includes/

Unstaged changes:
    Modified:   analysis/_site.yml

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/starter.rmd) and HTML (docs/starter.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File Version Author Date Message
html 59de338 Ziang Zhang 2024-12-06 Build site.
html 80526a6 Ziang Zhang 2024-11-26 Build site.
Rmd f0f969a Ziang Zhang 2024-11-26 workflowr::wflow_publish("analysis/starter.rmd")
html b35e5c9 Ziang Zhang 2024-11-26 Build site.
Rmd 62f1a67 Ziang Zhang 2024-11-26 workflowr::wflow_publish("analysis/starter.rmd")
html 6be64e9 Ziang Zhang 2024-11-26 Build site.
Rmd 69ac6db Ziang Zhang 2024-11-26 workflowr::wflow_publish("analysis/starter.rmd")
html 287b798 Ziang Zhang 2024-11-24 Build site.
Rmd 1709c74 Ziang Zhang 2024-11-24 workflowr::wflow_publish("analysis/starter.rmd")
html fa8c8ed Ziang Zhang 2024-11-21 Build site.
html 563118f Ziang Zhang 2024-11-21 Build site.
html daac389 Ziang Zhang 2024-11-21 Build site.
html 96b32c6 Ziang Zhang 2024-11-21 Build site.
Rmd 1a0cfcb Ziang Zhang 2024-11-21 workflowr::wflow_publish("analysis/starter.rmd")
html c4bd829 Ziang Zhang 2024-11-21 Build site.
Rmd 7fb7a81 Ziang Zhang 2024-11-21 workflowr::wflow_publish("analysis/starter.rmd") 
library(BayesGP)
library(tidyverse)
library(parallel)
source("code/functions.R")

A Synthetic Dataset

In this tutorial, we introduce the basic steps to fit a sGP model using the seasonal B-spline approximation introduced in Zhang et al, 2024.

For illustration, we use one of the synthetic datasets described in the main paper. The dataset and its corresponding true function are shown in the plots below.

n <- 500
location_of_interest <- seq(0, 10, length.out = 500)
true_f <- function(x){
  if(x < 2){
    return(2*sin(2 * 2 * pi * x) * (3-x))
  } else if (x > 2 && x < 4){
    return(2*sin(2 * 2 * pi * x))
  } else{
    return(2*sin(2 * 2 * pi * x) * (log(x-3) + 1))
  }
}
true_f <- Vectorize(true_f)

set.seed(123)
data <- simulate_data_poisson(func = true_f, n = n, sigma = 0.5, region = c(0,10), offset = 0)

par(mfrow = c(1,2))
plot(data$x, data$y, type = "p", col = "black", 
     pch = 20, cex = 0.5,
     ylab = "y", xlab = "x")
lines(location_of_interest, exp(true_f(location_of_interest)), col = "red", lwd = 2)
plot(location_of_interest, true_f(location_of_interest),
     type = "l", col = "black",
     pch = 20, cex = 0.5,
     ylab = "y", xlab = "x")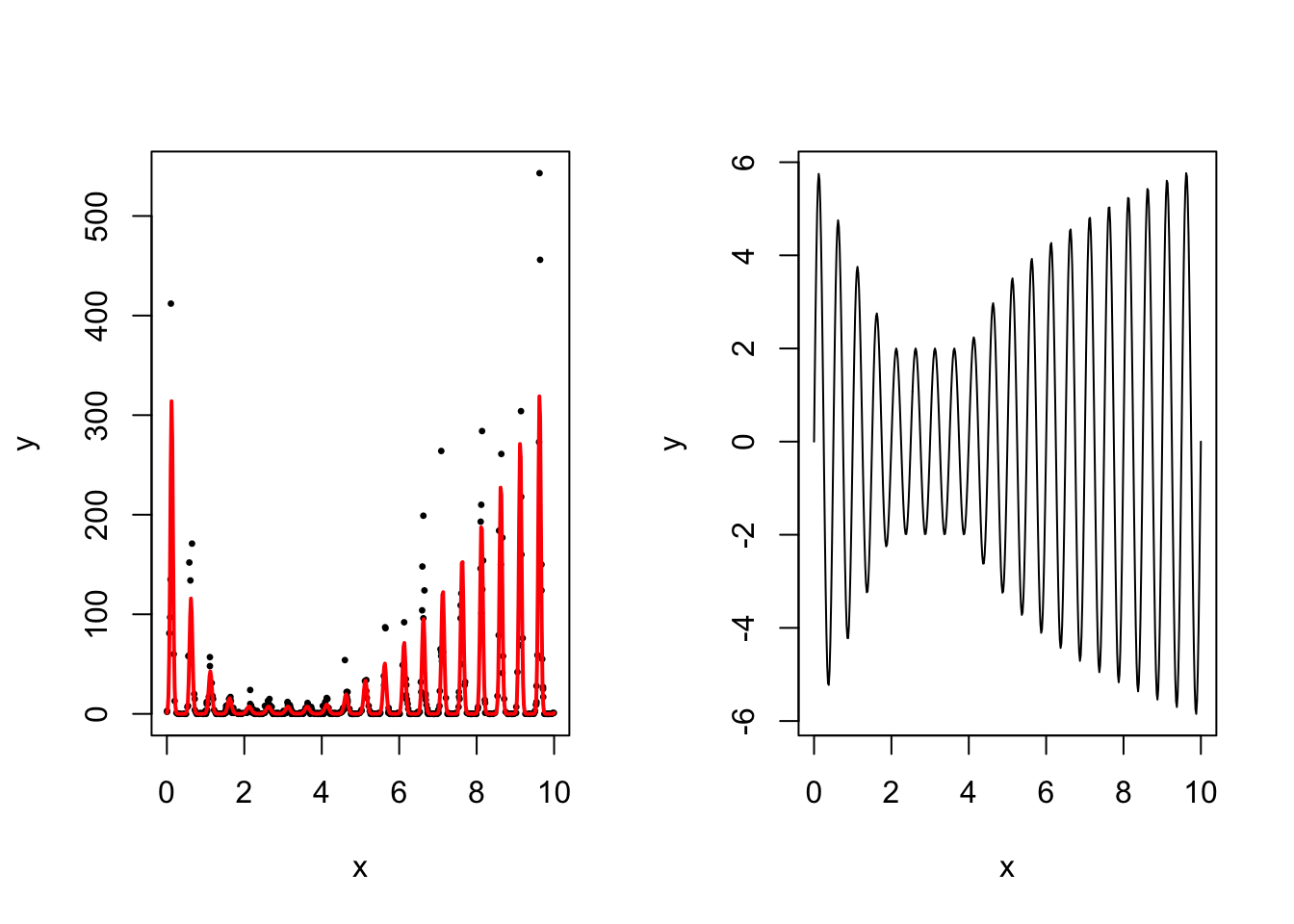

Version Author Date
c4bd829 Ziang Zhang 2024-11-21 
par(mfrow = c(1,1))

The hierarchical model we consider is as follows:

\[\begin{equation} \begin{aligned} Y_i|x_i,\xi_i &\sim \text{Poisson}(\lambda_i), \\ \text{log}(\lambda_i) &= \beta_0 + g(x_i) + \xi_i, \\ g(x) &\sim \text{sGP}_{\alpha}(\sigma_x), \\ \xi_i &\sim \text{N}(0, \sigma_\xi^2). \end{aligned} \end{equation}\]

We assume the sGP prior has a frequency of \(2\) (\(\alpha = 4\pi\)), and use an Exponential prior for the one-step PSD \(\sigma(1)\) defined as: \[ \text{P}(\sigma(1) > 2) = 0.1, \] which corresponds to a prior median of:

INLA::inla.pc.qprec(0.5, u=2, alpha = 0.1)^{-0.5}
[1] 0.60206

The standard deviation \(\sigma_\xi\) of the observation-level random intercept that accounts for the overdispersion, follows an Exponential prior with a median of \(1\). All the fixed effects (including the boundary effects of the sGP) are assigned independent normal priors with zero mean and variance \(1000\).

To make the computation more efficient, we will use \(10\) equally spaced knots to define the B-spline basis, which will then be used to approximate the sGP prior.

Inference using BayesGP

To make approximate Bayesian inference of the above model, we make use of the BayesGP package.

The main function to fit the model is model_fit, which takes a formula, a dataset, and a family as input.

We specify the sGP prior by using the f function in the formula, and set the model argument to "sgp".

The region argument specifies the region where the FEM approximation is defined, which by default is the same as the range of the covariate.

The prior for the standard deviation parameter of the GP or the random effect is specified by the sd.prior argument. When sd.prior is a list, specifying the h argument will automatically convert the SD to the \(h\)-step PSD. When sd.prior is specified as a scalar, it is assumed to be prior median.

Below is an example of fitting the model to the synthetic dataset:

mod <- BayesGP::model_fit(
    y ~ f(
      x,
      model = "sgp",
      region = c(0,10),
      freq = 2,
      k = 10, # number of knots
      sd.prior = list(param = list(u = 2, alpha = 0.1), h = 1)
    ) +
      f(index, model = "iid", sd.prior = 1),
    data = data,
    family = "Poisson"
  )

Note that specifying freq = 2 is equivalent to setting a = 4*pi which is also equivalent to setting period = 1/2 in the sGP prior.

We can take a quick look at the posterior summary:

summary(mod)
Here are some posterior/prior summaries for the parameters: 
        name median q0.025 q0.975       prior prior:P1 prior:P2
1  intercept  0.108 -0.052  0.274      Normal        0    1e+03
2    x (PSD)  0.890  0.636  1.342 Exponential        2    1e-01
3 index (SD)  0.485  0.423  0.556 Exponential        1    5e-01
For Normal prior, P1 is its mean and P2 is its variance. 
For Exponential prior, prior is specified as P(theta > P1) = P2.

We can also obtain the posterior of \(g\) at any location of interest:

post_g <- predict(mod, newdata = data.frame(x = location_of_interest), variable = "x", include.intercept = FALSE)
head(post_g)
           x     q0.025      q0.5    q0.975     mean
1 0.00000000 -0.2694881 0.1600508 0.5893843 0.159338
2 0.02004008  1.1280252 1.5363202 1.9418746 1.536748
3 0.04008016  2.4315792 2.8178895 3.2127484 2.815710
4 0.06012024  3.5301288 3.9165008 4.2996541 3.914358
5 0.08016032  4.3697162 4.7602353 5.1481787 4.762672
6 0.10020040  4.9049295 5.3075811 5.6994210 5.307025

Take a look at the plot of them:

plot(location_of_interest, true_f(location_of_interest),
     type = "l", col = "black",
     pch = 20, cex = 0.5,
     ylab = "y", xlab = "x")
lines(x = location_of_interest, y = (post_g$mean), col = "blue", lwd = 1, lty = 2)
polygon(c(location_of_interest, rev(location_of_interest)),
        c(post_g$q0.025, rev(post_g$q0.975)),
        col = adjustcolor("blue", alpha.f = 0.2), border = NA)
legend("topright", legend = c("True function", "Posterior mean"),
       col = c("black", "blue"), lty = c(1, 2), lwd = c(1, 1))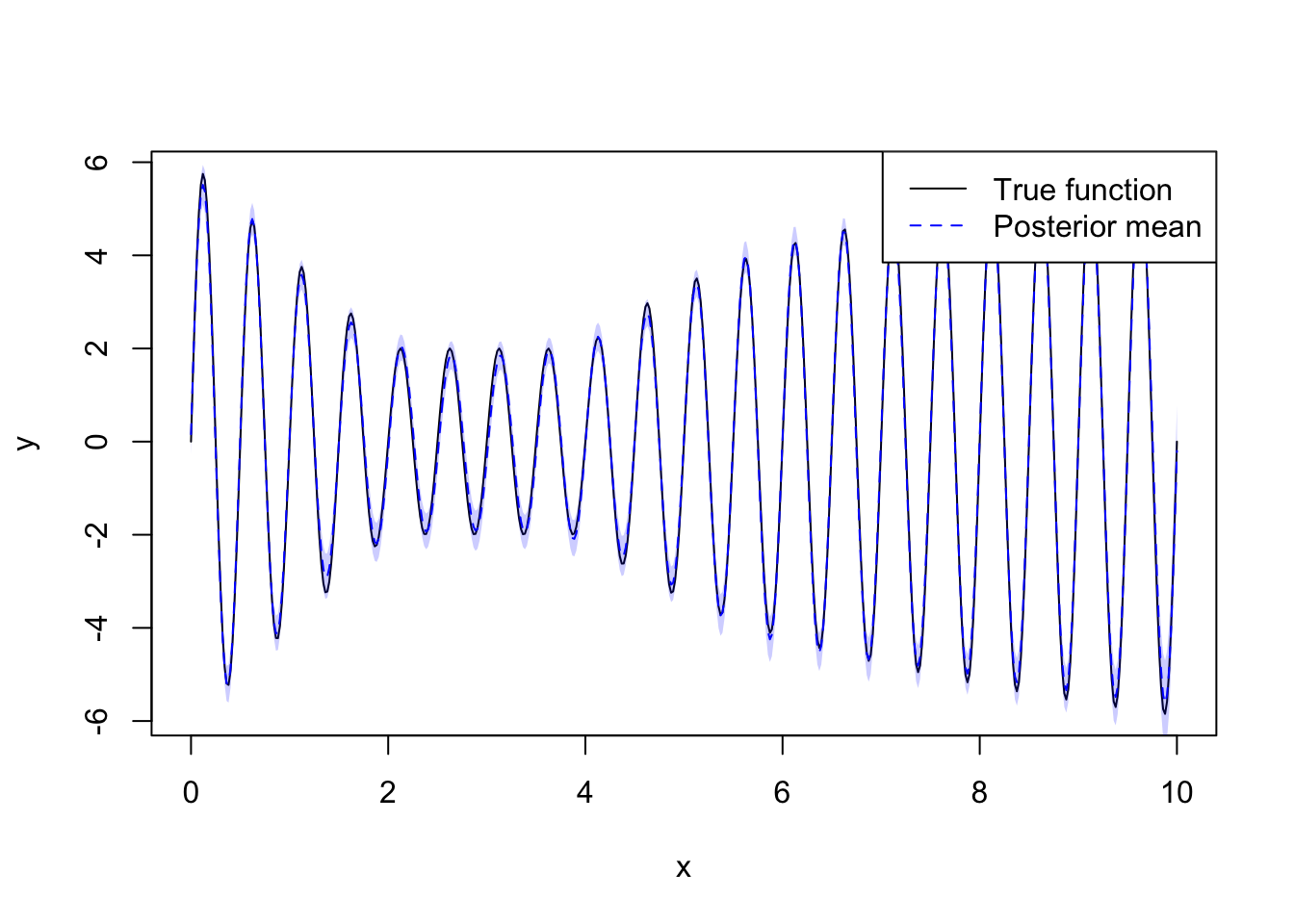

Version Author Date
6be64e9 Ziang Zhang 2024-11-26
287b798 Ziang Zhang 2024-11-24
c4bd829 Ziang Zhang 2024-11-21

The quantiles reported from predict can be easily modified by setting the quantiles argument. For example, to obtain the \(0.05\) and \(0.95\) quantiles, we can set quantiles = c(0.05, 0.95).

post_g <- predict(mod, newdata = data.frame(x = location_of_interest), variable = "x", include.intercept = FALSE, quantiles = c(0.05, 0.95))
head(post_g)
           x      q0.05     q0.95     mean
1 0.00000000 -0.2078407 0.5136182 0.159338
2 0.02004008  1.1933600 1.8852268 1.536748
3 0.04008016  2.4888903 3.1356789 2.815710
4 0.06012024  3.5991912 4.2339789 3.914358
5 0.08016032  4.4427572 5.0866405 4.762672
6 0.10020040  4.9670371 5.6440898 5.307025

We can also just obtain the posterior samples of \(g\) at these locations:

post_g_raw <- predict(mod, newdata = data.frame(x = location_of_interest), variable = "x", only.samples = TRUE, include.intercept = FALSE)
plot(location_of_interest, true_f(location_of_interest),
     type = "l", col = "black",
     pch = 20, cex = 0.5,
     ylab = "y", xlab = "x")
matlines(location_of_interest, post_g_raw[,2:12], col = "pink", lty = 2, lwd = 0.5)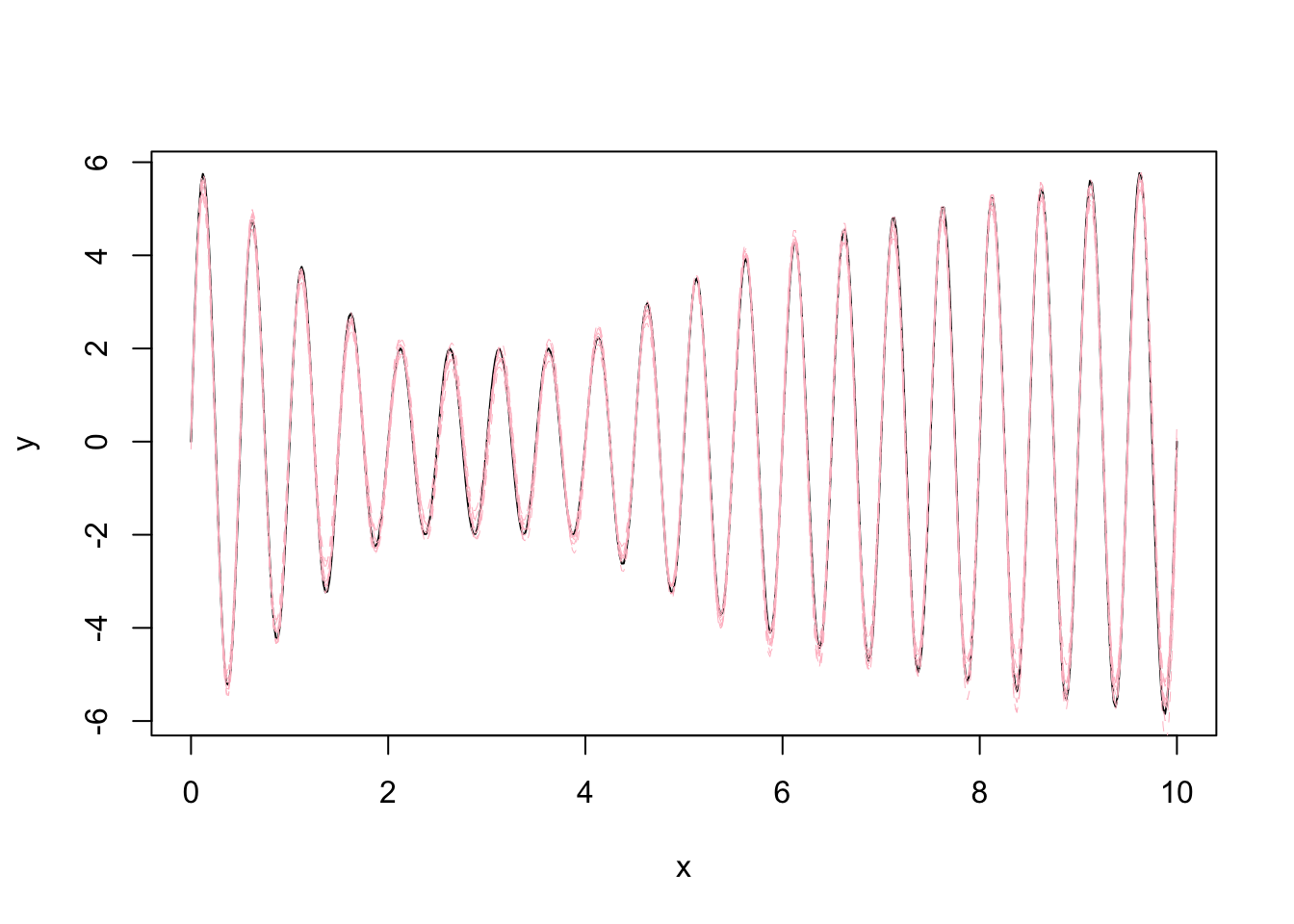

Version Author Date
6be64e9 Ziang Zhang 2024-11-26 

sessionInfo()
R version 4.3.1 (2023-06-16)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.7.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Chicago
tzcode source: internal

attached base packages:
[1] parallel  stats     graphics  grDevices utils     datasets  methods  
[8] base     

other attached packages:
 [1] lubridate_1.9.3 forcats_1.0.0   stringr_1.5.1   dplyr_1.1.4    
 [5] purrr_1.0.2     readr_2.1.5     tidyr_1.3.1     tibble_3.2.1   
 [9] ggplot2_3.5.1   tidyverse_2.0.0 BayesGP_0.1.3   workflowr_1.7.1

loaded via a namespace (and not attached):
 [1] tidyselect_1.2.1    hdrcde_3.4          bitops_1.0-9       
 [4] fastmap_1.2.0       RCurl_1.98-1.16     INLA_23.09.09      
 [7] pracma_2.4.4        promises_1.3.0      digest_0.6.37      
[10] timechange_0.3.0    lifecycle_1.0.4     sf_1.0-17          
[13] cluster_2.1.6       statmod_1.5.0       processx_3.8.4     
[16] magrittr_2.0.3      compiler_4.3.1      rlang_1.1.4        
[19] sass_0.4.9          tools_4.3.1         utf8_1.2.4         
[22] yaml_2.3.10         data.table_1.16.2   knitr_1.48         
[25] sp_2.1-4            mclust_6.1.1        classInt_0.4-10    
[28] rainbow_3.8         KernSmooth_2.23-24  fda_6.2.0          
[31] numDeriv_2016.8-1.1 withr_3.0.2         grid_4.3.1         
[34] pcaPP_2.0-5         fansi_1.0.6         git2r_0.33.0       
[37] e1071_1.7-16        colorspace_2.1-1    scales_1.3.0       
[40] MASS_7.3-60         cli_3.6.3           mvtnorm_1.3-1      
[43] rmarkdown_2.28      generics_0.1.3      mvQuad_1.0-8       
[46] rstudioapi_0.16.0   httr_1.4.7          tzdb_0.4.0         
[49] fds_1.8             DBI_1.2.3           cachem_1.1.0       
[52] proxy_0.4-27        splines_4.3.1       aghq_0.4.1         
[55] vctrs_0.6.5         Matrix_1.6-4        jsonlite_1.8.9     
[58] callr_3.7.6         hms_1.1.3           jquerylib_0.1.4    
[61] units_0.8-5         glue_1.8.0          ps_1.8.0           
[64] stringi_1.8.4       gtable_0.3.6        later_1.3.2        
[67] munsell_0.5.1       pillar_1.9.0        htmltools_0.5.8.1  
[70] deSolve_1.40        TMB_1.9.15          R6_2.5.1           
[73] fmesher_0.1.7       ks_1.14.3           rprojroot_2.0.4    
[76] evaluate_1.0.1      lattice_0.22-6      highr_0.11         
[79] httpuv_1.6.15       bslib_0.8.0         class_7.3-22       
[82] Rcpp_1.0.13-1       whisker_0.4.1       xfun_0.48          
[85] fs_1.6.4            getPass_0.2-4       pkgconfig_2.0.3