Last updated: 2025-07-10

Checks: 7 0

Knit directory: InferOrder/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20250707)

The command set.seed(20250707) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 3298282

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 3298282. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store

Unstaged changes:
    Modified:   analysis/explore_pancrea.rmd
    Modified:   code/general_EM.R
    Modified:   code/general_EM_obs.R
    Modified:   code/linear_EM.R

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/explore_smoothEM.rmd) and HTML (docs/explore_smoothEM.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File Version Author Date Message
Rmd 3298282 Ziang Zhang 2025-07-10 workflowr::wflow_publish("analysis/explore_smoothEM.rmd")
Rmd 041218f Ziang Zhang 2025-07-09 add result using smoothEM
html 041218f Ziang Zhang 2025-07-09 add result using smoothEM
html 2322978 Ziang Zhang 2025-07-08 Build site.
html 028201f Ziang Zhang 2025-07-08 Build site.
Rmd ccaa320 Ziang Zhang 2025-07-07 workflowr::wflow_publish("analysis/explore_smoothEM.rmd")

Introduction

In this study, we consider a mixture model with \(K\) components, specified as follows: \[\begin{equation} \label{eq:smooth-EM} \begin{aligned} \boldsymbol{X}_i \mid z_i = k &\sim \mathcal{N}(\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \quad i\in [n], \\ \boldsymbol{U} = (\boldsymbol{\mu}_1, \ldots, \boldsymbol{\mu}_K) &\sim \mathcal{N}(\boldsymbol{0}, \mathbf{Q}^{-1}), \end{aligned} \end{equation}\] where \(\boldsymbol{X}_i \in \mathbb{R}^d\) denotes the observed data, \(z_i \in [K]\) is a latent indicator assigning observation \(i\) to component \(k\), \(\boldsymbol{\mu}_k \in \mathbb{R}^d\) is the mean vector of component \(k\), and \(\boldsymbol{\Sigma}_k \in \mathbb{R}^{d\times d}\) is its covariance matrix.

The prior distribution over the stacked mean vectors \(\boldsymbol{U}\) is multivariate normal with mean zero and precision matrix \(\mathbf{Q}\). This prior can encode smoothness or structural assumptions about how the component means evolve or are ordered (e.g., spatial or temporal constraints across \(k=1,\ldots,K\)).

Rather than using the standard EM algorithm, we employ a smooth-EM approach that incorporates this structured prior over component means. In this framework:

  • E-step (standard): \[ \gamma_{ik}^{(t)} = \frac{\pi_k^{(t)} \, \mathcal{N}(\boldsymbol{X}_i \mid \boldsymbol{\mu}_k^{(t)}, \boldsymbol{\Sigma}_k^{(t)})}{\sum_{j=1}^K \pi_j^{(t)} \, \mathcal{N}(\boldsymbol{X}_i \mid \boldsymbol{\mu}_j^{(t)}, \boldsymbol{\Sigma}_j^{(t)})}. \]

  • M-step (incorporating prior): \[ \begin{aligned} \{\pi^{(t+1)}, \mathbf{U}^{(t+1)}, \boldsymbol{\Sigma}^{(t+1)}\} &= \arg\max \, \mathbb{E}_{\gamma^{(t)}}\Big[\log p(\boldsymbol{X}, \mathbf{U}, \mathbf{Z} \mid \pi, \boldsymbol{\Sigma})\Big] \\ &= \arg\max \, \mathbb{E}_{\gamma^{(t)}}\Big[\log p(\boldsymbol{X}, \mathbf{Z} \mid \pi, \mathbf{U}, \boldsymbol{\Sigma}) + \log p(\mathbf{U})\Big] \\ &= \arg\max \, \bigg\{\mathbb{E}_{\gamma^{(t)}}\Big[\log p(\boldsymbol{X}, \mathbf{Z} \mid \pi, \mathbf{U}, \boldsymbol{\Sigma})\Big] - \frac{1}{2} \mathbf{U}^\top \mathbf{Q} \mathbf{U}\bigg\} \\ &= \arg\max \, \left\{ -\frac{1}{2} \sum_{i,k} \gamma_{ik}^{(t)} \|\boldsymbol{X}_i - \boldsymbol{\mu}_k\|^2_{\boldsymbol{\Sigma}_k^{-1}} - \frac{1}{2} \mathbf{U}^\top \mathbf{Q} \mathbf{U}\right\}. \end{aligned} \]

Unlike the standard EM algorithm, which maximizes the likelihood independently over component means, the smooth-EM algorithm performs MAP estimation that considers the prior of \(\boldsymbol{U}\), encouraging ordered or smooth transitions across components indexed by \(k\).

We will now explore how this smooth-EM algorithm behaves under different prior specifications for \(\mathbf{Q}\).

Simulate mixture in 2D

Here, we will simulate a mixture of Gaussians in 2D, for \(n = 500\) observations and \(K = 5\) components.

source("./code/simulate.R")
library(MASS)
library(mvtnorm)
Warning: package 'mvtnorm' was built under R version 4.3.3
palette_colors <- rainbow(5)
alpha_colors <- sapply(palette_colors, function(clr) adjustcolor(clr, alpha.f=0.3))
sim <- simulate_mixture(n=500, K = 5, d=2, seed=123, proj_mat = matrix(c(1,-0.6,-0.6,1), nrow = 2, byrow = T))
plot(sim$X, col = alpha_colors[sim$z],
     pch = 19, cex = 0.5, 
     xlab = "X1", ylab = "X2",
     main = "Simulated mixture of Gaussians in 2D")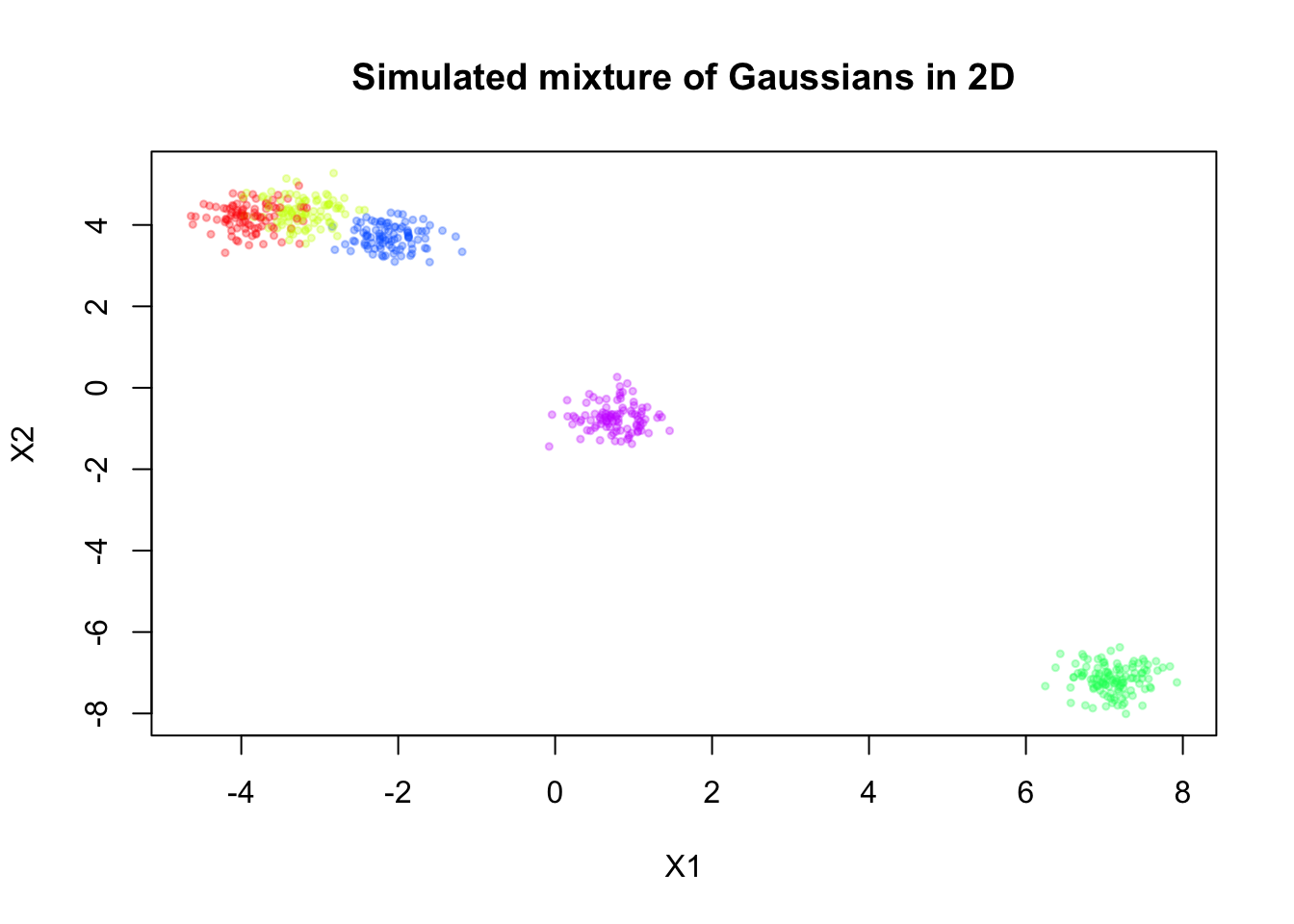

Version Author Date
028201f Ziang Zhang 2025-07-08

Now, let’s assume we don’t know there are five components, and we will fit a mixture model with \(K = 20\) components to this data. For simplicity, let’s assume \(\mathbf{\Sigma}_k = \sigma^2 \mathbf{I}\) for all \(k\), where \(\sigma^2\) is a constant variance across components.

Fitting regular EM

First, we fit the standard EM algorithm to this mixture model without any prior on the means.

library(mclust)
Package 'mclust' version 6.1.1
Type 'citation("mclust")' for citing this R package in publications.

Attaching package: 'mclust'
The following object is masked from 'package:mvtnorm':

    dmvnorm
fit_mclust <- Mclust(sim$X, G=20, modelNames = "EEI")
plot(sim$X, col=alpha_colors[sim$z],
     xlab="X1", ylab="X2",
     cex=0.5, pch=19, main="mclust")
mclust_means <- t(fit_mclust$parameters$mean)
points(mclust_means, pch=3, cex=2, lwd=2, col="red")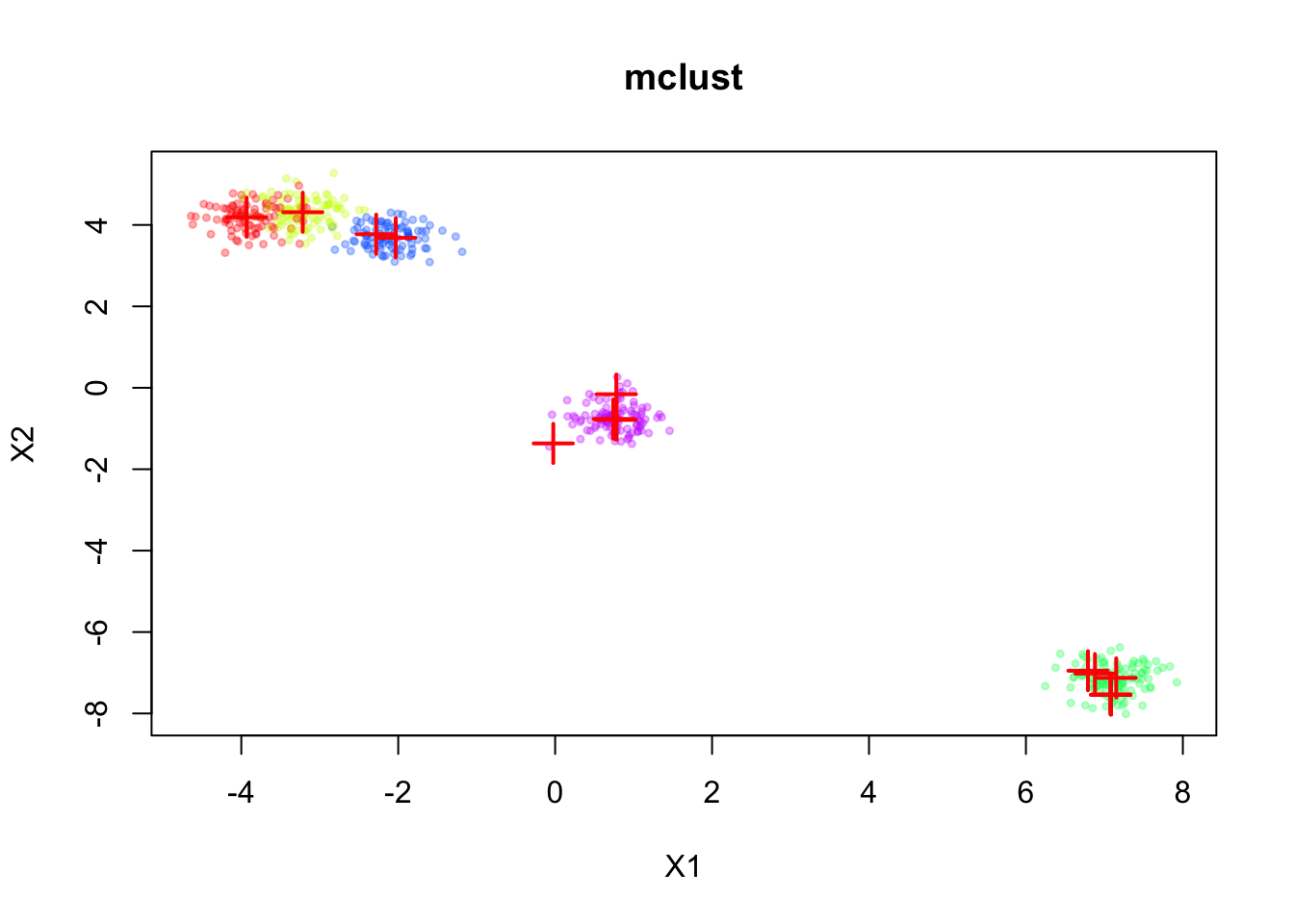

Version Author Date
028201f Ziang Zhang 2025-07-08

The inferred means are shown in red. We can see that the means are well aligned with the true component means, but we don’t have a natural ordering of the means.

Fitting smooth-EM with a linear prior

We consider the simplest case for the prior on the component means \(\mathbf{U}\), where \(\mathbf{Q}\) corresponds to a linear trend prior. Specifically, we assume that \[ \boldsymbol{\mu}_k = l_k \boldsymbol{\beta}, \] for some shared slope vector \(\boldsymbol{\beta} \in \mathbb{R}^d\), with \(\{l_k\}\) being equally spaced values increasing from \(-1\) to \(1\).

source("./code/linear_EM.R")
source("./code/general_EM.R")
Warning: package 'matrixStats' was built under R version 4.3.3
result_linear <- EM_algorithm_linear(
  data = sim$X,
  K = 20,
  betaprec = 0.001,
  seed = 123,
  max_iter = 100,
  verbose = TRUE
)
Iteration   1: objective = -2741.247096
Iteration   2: objective = -2556.265957
Iteration   3: objective = -2368.973053
Iteration   4: objective = -2159.332551
Iteration   5: objective = -1872.947089
Iteration   6: objective = -1586.908025
Iteration   7: objective = -1382.252276
Iteration   8: objective = -1277.268346
Iteration   9: objective = -1236.296149
Iteration  10: objective = -1218.570070
Iteration  11: objective = -1210.506912
Iteration  12: objective = -1206.925206
Iteration  13: objective = -1205.281111
Iteration  14: objective = -1204.472725
Iteration  15: objective = -1204.051511
Iteration  16: objective = -1203.822996
Iteration  17: objective = -1203.695380
Iteration  18: objective = -1203.622527
Iteration  19: objective = -1203.580213
Iteration  20: objective = -1203.555297
Iteration  21: objective = -1203.540464
Iteration  22: objective = -1203.531557
Iteration  23: objective = -1203.526170
Iteration  24: objective = -1203.522895
Iteration  25: objective = -1203.520894
Iteration  26: objective = -1203.519669
Iteration  27: objective = -1203.518915
Iteration  28: objective = -1203.518452
Iteration  29: objective = -1203.518166
Iteration  30: objective = -1203.517989
Iteration  31: objective = -1203.517880
Iteration  32: objective = -1203.517813
Converged at iteration 32 with objective -1203.517813
plot(sim$X, col=alpha_colors[sim$z], cex=1,
     pch=19, main="EM Fitted Means with linear Prior")
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, as.vector(result_linear$params$mu))
# Draw arrows showing sequence
for (k in 1:(nrow(mu_matrix)-1)) {
  arrows(mu_matrix[k,1], mu_matrix[k,2],
         mu_matrix[k+1,1], mu_matrix[k+1,2],
         col="orange", lwd=4, length=0.1)
}
# add dots for fitted means
points(mu_matrix, pch=1, cex=0.8, lwd=2, col="orange")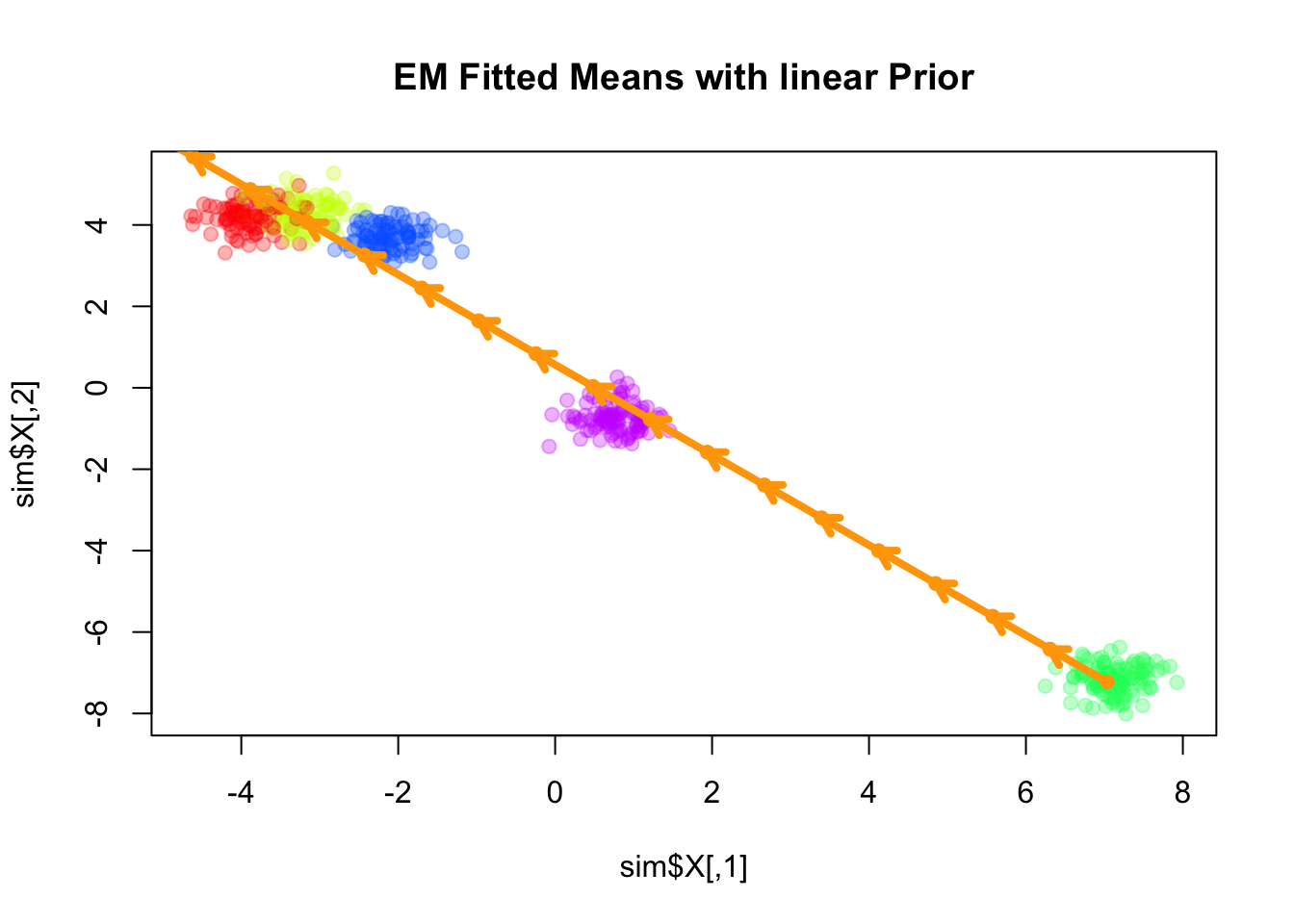

Version Author Date
041218f Ziang Zhang 2025-07-09
028201f Ziang Zhang 2025-07-08

Here the fitted means are shown as orange arrows, with direction indicating the order of the components.

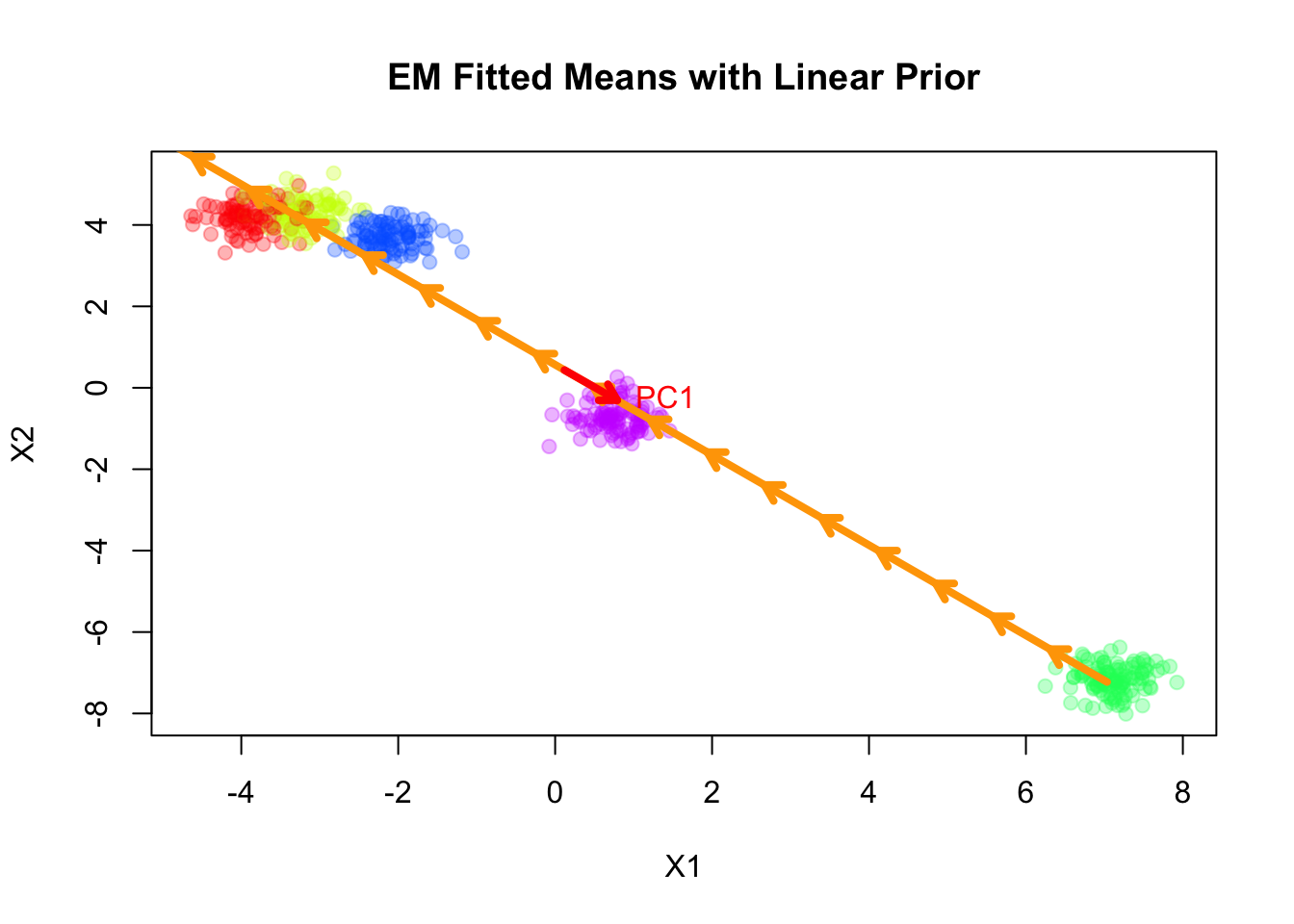
Note that the fitted slope \(\boldsymbol{\beta}\) is very close to the first principal component of the data.

plot(sim$X, col=alpha_colors[sim$z], cex=1,
     xlab="X1", ylab="X2",
     pch=19, main="EM Fitted Means with Linear Prior")
     
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, result_linear$params$mu)

# Draw arrows showing sequence of cluster means
for (k in 1:(nrow(mu_matrix)-1)) {
  if (sqrt(sum((mu_matrix[k+1,] - mu_matrix[k,])^2)) > 1e-6) {
    arrows(mu_matrix[k,1], mu_matrix[k,2],
           mu_matrix[k+1,1], mu_matrix[k+1,2],
           col="orange", lwd=4, length=0.1)
  }
}

# ====== Fit PCA ======
pca_fit <- prcomp(sim$X, center=TRUE, scale.=FALSE)
pcs <- pca_fit$rotation  # columns are PC directions
X_center <- colMeans(sim$X)

# Set radius for arrows
radius <- 1

# ====== Draw PC arrows ======
arrows(
  X_center[1], X_center[2],
  X_center[1] + radius * pcs[1,1],
  X_center[2] + radius * pcs[2,1],
  col="red", lwd=4, length=0.1
)
text(
  X_center[1] + radius * pcs[1,1],
  X_center[2] + radius * pcs[2,1],
  labels="PC1", pos=4, col="red"
)

Version Author Date
041218f Ziang Zhang 2025-07-09
028201f Ziang Zhang 2025-07-08

Fitting smooth-EM with a VAR(1) prior

Next, we consider a first-order vector autoregressive (VAR(1)) prior on the component means. Under this prior, each component mean \(\boldsymbol{\mu}_k\) depends linearly on its immediate predecessor \(\boldsymbol{\mu}_{k-1}\), with Gaussian noise: \[ \begin{aligned} \boldsymbol{\mu}_k &= \mathbf{A} \boldsymbol{\mu}_{k-1} + \boldsymbol{\epsilon}_k, \\ \boldsymbol{\epsilon}_k &\sim \mathcal{N}(\mathbf{0}, \mathbf{Q}_\epsilon^{-1}), \end{aligned} \] where \(\mathbf{A}\) is the transition matrix encoding the dependence of the current mean on the previous mean, and \(\mathbf{Q}_\epsilon\) is the precision matrix of the noise term.

Let’s for now assume the transition matrix \(\mathbf{A}\) and the noise precision matrix \(\mathbf{Q}_\epsilon\) are given by:

\[ \mathbf{A} = 0.8 \, \mathbf{I}_2 \] \[ \mathbf{Q}_\epsilon = 0.1 \, \mathbf{I}_2 \]

where \(\mathbf{I}_2\) is the 2-dimensional identity matrix.

source("./code/prior_precision.R")
Q_prior_VAR1 <- make_VAR1_precision(K=20, d=2, A = diag(2) * 0.8, Q = diag(2) * 0.1)
set.seed(1)
init_params <- make_default_init(sim$X, K=20)
result_VAR1 <- EM_algorithm(
  data = sim$X,
  Q_prior = Q_prior_VAR1,
  init_params = init_params,
  max_iter = 100,
  modelName = "EEI",
  tol = 1e-3,
  verbose = TRUE
)
Iteration   1: objective = -1816.061482
Iteration   2: objective = -1584.739929
Iteration   3: objective = -1476.102618
Iteration   4: objective = -1402.112627
Iteration   5: objective = -1401.647535
Iteration   6: objective = -1401.536854
Iteration   7: objective = -1401.377684
Iteration   8: objective = -1401.143065
Iteration   9: objective = -1400.794563
Iteration  10: objective = -1400.275018
Iteration  11: objective = -1399.499366
Iteration  12: objective = -1398.341404
Iteration  13: objective = -1396.613967
Iteration  14: objective = -1394.037634
Iteration  15: objective = -1390.187887
Iteration  16: objective = -1384.401471
Iteration  17: objective = -1375.611192
Iteration  18: objective = -1362.103523
Iteration  19: objective = -1341.553522
Iteration  20: objective = -1312.517496
Iteration  21: objective = -1277.611360
Iteration  22: objective = -1248.488954
Iteration  23: objective = -1234.630112
Iteration  24: objective = -1230.153804
Iteration  25: objective = -1228.759121
Iteration  26: objective = -1228.280403
Iteration  27: objective = -1228.092926
Iteration  28: objective = -1228.003670
Iteration  29: objective = -1227.949442
Iteration  30: objective = -1227.907899
Iteration  31: objective = -1227.870447
Iteration  32: objective = -1227.833512
Iteration  33: objective = -1227.795485
Iteration  34: objective = -1227.755549
Iteration  35: objective = -1227.713217
Iteration  36: objective = -1227.668129
Iteration  37: objective = -1227.619966
Iteration  38: objective = -1227.568416
Iteration  39: objective = -1227.513155
Iteration  40: objective = -1227.453845
Iteration  41: objective = -1227.390136
Iteration  42: objective = -1227.321674
Iteration  43: objective = -1227.248120
Iteration  44: objective = -1227.169174
Iteration  45: objective = -1227.084618
Iteration  46: objective = -1226.994367
Iteration  47: objective = -1226.898541
Iteration  48: objective = -1226.797545
Iteration  49: objective = -1226.692138
Iteration  50: objective = -1226.583467
Iteration  51: objective = -1226.473012
Iteration  52: objective = -1226.362453
Iteration  53: objective = -1226.253512
Iteration  54: objective = -1226.147997
Iteration  55: objective = -1226.048246
Iteration  56: objective = -1225.957755
Iteration  57: objective = -1225.881081
Iteration  58: objective = -1225.822064
Iteration  59: objective = -1225.781393
Iteration  60: objective = -1225.756125
Iteration  61: objective = -1225.741639
Iteration  62: objective = -1225.733763
Iteration  63: objective = -1225.729610
Iteration  64: objective = -1225.727451
Iteration  65: objective = -1225.726332
Iteration  66: objective = -1225.725747
Converged at iteration 66 with objective -1225.725747
plot(sim$X, col=alpha_colors[sim$z], cex=1,
     xlab="X1", ylab="X2",
     pch=19, main="EM Fitted Means with VAR(1) Prior")
     
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, result_VAR1$params$mu)

# Draw arrows showing sequence of cluster means
for (k in 1:(nrow(mu_matrix)-1)) {
  if (sqrt(sum((mu_matrix[k+1,] - mu_matrix[k,])^2)) > 1e-6) {
    arrows(mu_matrix[k,1], mu_matrix[k,2],
           mu_matrix[k+1,1], mu_matrix[k+1,2],
           col="orange", lwd=4, length=0.1)
  }
}
points(mu_matrix, pch=8, cex=1, lwd=1, col="orange")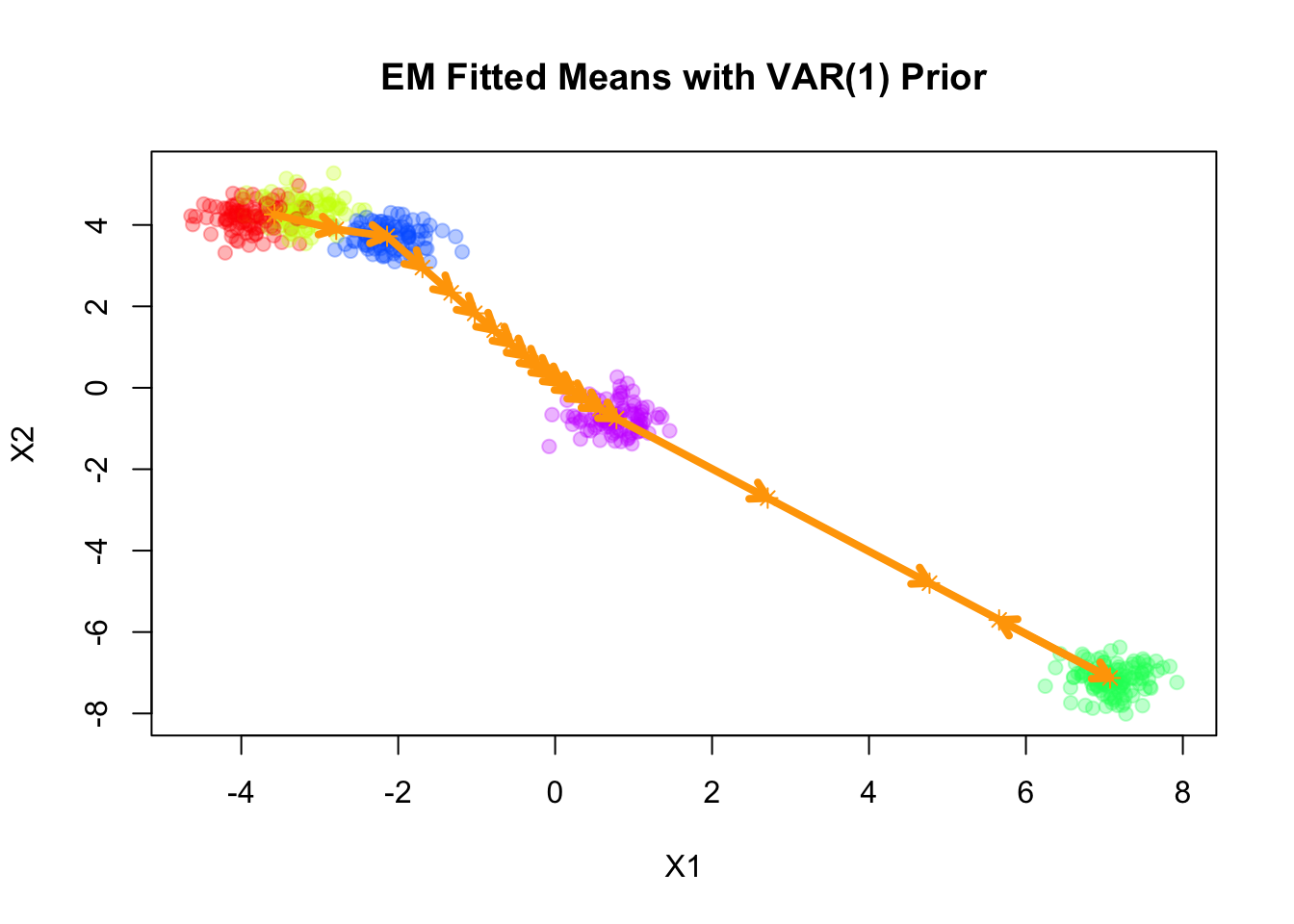

Version Author Date
028201f Ziang Zhang 2025-07-08

Fitting smooth-EM with a RW1 prior

Next, we consider a first-order random walk (RW1) prior on the component means, formulated using the difference operator. Under this prior, successive differences of the means are modeled as independent Gaussian noise:

\[ \Delta \boldsymbol{\mu}_k = \boldsymbol{\mu}_k - \boldsymbol{\mu}_{k-1} \sim \mathcal{N}\big(\mathbf{0}, \lambda^{-1} \mathbf{I}_d\big), \]

where \(\lambda\) is a scalar precision parameter that controls the smoothness of the mean sequence. Larger values of \(\lambda\) enforce stronger smoothness by penalizing large differences between successive component means.

Q_prior_RW1 <- make_random_walk_precision(K=20, d=2, lambda = 10)
result_RW1 <- EM_algorithm(
  data = sim$X,
  Q_prior = Q_prior_RW1,
  init_params = init_params,
  max_iter = 100,
  modelName = "EEI",
  tol = 1e-3,
  verbose = TRUE
)
Iteration   1: objective = -1687.103780
Iteration   2: objective = -1476.193798
Iteration   3: objective = -1353.226437
Iteration   4: objective = -1313.555728
Iteration   5: objective = -1312.645222
Iteration   6: objective = -1309.586061
Iteration   7: objective = -1299.026583
Iteration   8: objective = -1276.794786
Iteration   9: objective = -1242.036484
Iteration  10: objective = -1197.177730
Iteration  11: objective = -1161.014374
Iteration  12: objective = -1150.538792
Iteration  13: objective = -1149.417363
Iteration  14: objective = -1149.307137
Iteration  15: objective = -1149.293956
Iteration  16: objective = -1149.292130
Iteration  17: objective = -1149.291739
Converged at iteration 17 with objective -1149.291739
plot(sim$X, col=alpha_colors[sim$z], cex=1,
     xlab="X1", ylab="X2",
     pch=19, main="EM Fitted Means with RW(1) Prior")
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, result_RW1$params$mu)
# Draw arrows showing sequence of cluster means
for (k in 1:(nrow(mu_matrix)-1)) {
  if (sqrt(sum((mu_matrix[k+1,] - mu_matrix[k,])^2)) > 1e-6) {
    arrows(mu_matrix[k,1], mu_matrix[k,2],
           mu_matrix[k+1,1], mu_matrix[k+1,2],
           col="orange", lwd=4, length=0.1)
  }
}
Warning in arrows(mu_matrix[k, 1], mu_matrix[k, 2], mu_matrix[k + 1, 1], :
zero-length arrow is of indeterminate angle and so skipped
points(mu_matrix, pch=8, cex=1, lwd=1, col="orange")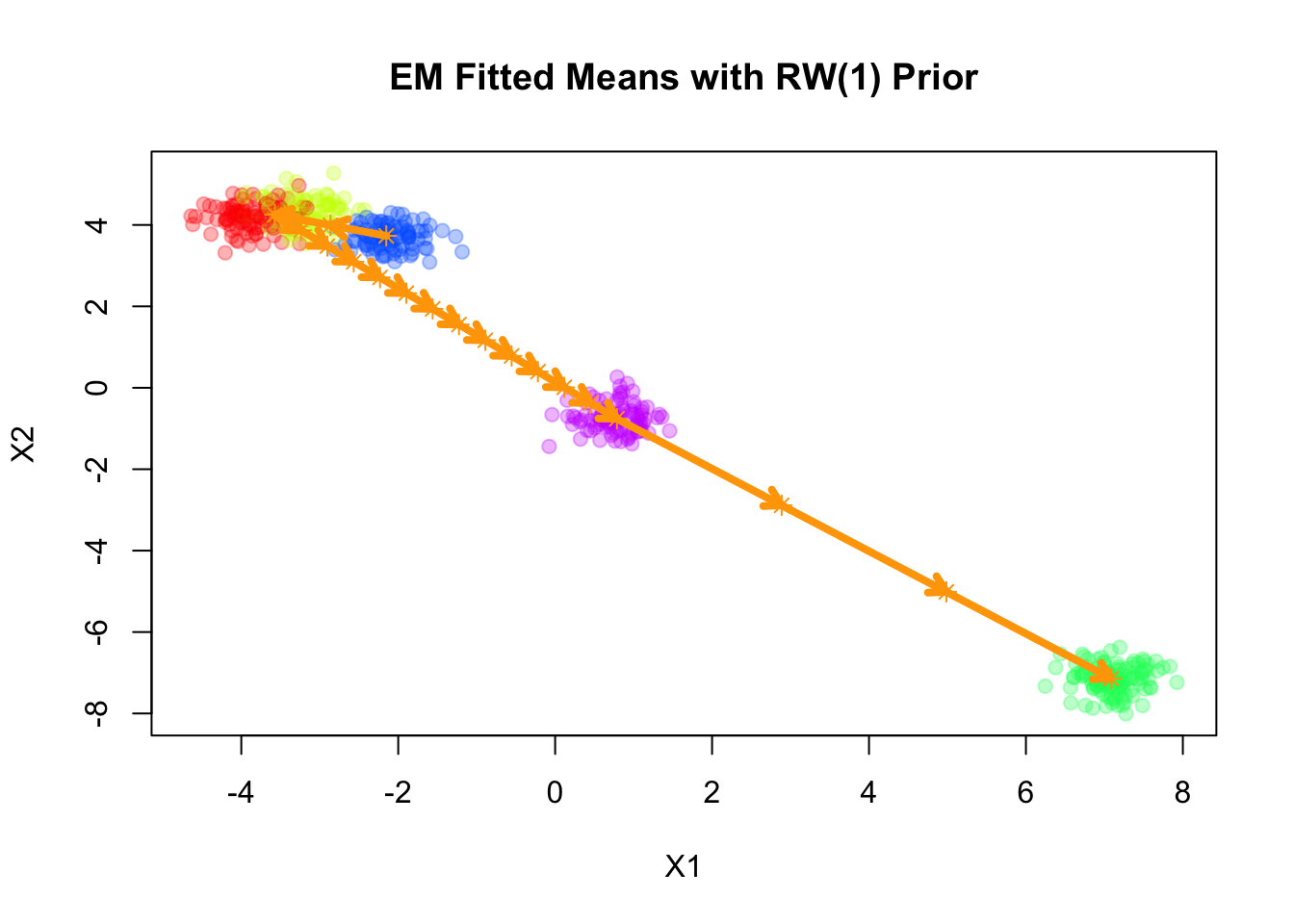

Version Author Date
041218f Ziang Zhang 2025-07-09
028201f Ziang Zhang 2025-07-08

The result of RW1 looks similar to that of VAR(1), which is not surprising since the RW1 prior is a special case of the VAR(1) prior with \(\mathbf{A} = \mathbf{I}\).

Note that RW1 is a partially improper prior, as the overall level of the means is not penalized. In other words, the prior is invariant to addition of any constant vector to all component means.

Fitting smooth-EM with a RW2 prior

Next, we consider a second-order random walk (RW2) prior on the component means, which penalizes the second differences of the means:

\[ \Delta^2 \boldsymbol{\mu}_k = \boldsymbol{\mu}_k - 2\boldsymbol{\mu}_{k-1} + \boldsymbol{\mu}_{k-2} \sim \mathcal{N}\big(\mathbf{0}, \lambda^{-1} \mathbf{I}_d\big), \]

where \(\Delta^2 \boldsymbol{\mu}_k\) denotes the second-order difference operator. The scalar precision parameter \(\lambda\) controls the smoothness of the sequence, with larger values enforcing stronger penalization of curvature.

Q_prior_rw2 <- make_random_walk_precision(K = 20, d = 2, q=2, lambda=400)
result_rw2 <- EM_algorithm(
  data = sim$X,
  Q_prior = Q_prior_rw2,
  init_params = init_params,
  max_iter = 100,
  modelName = "EEI",
  tol = 1e-3,
  verbose = TRUE
)
Iteration   1: objective = -3413.492461
Iteration   2: objective = -1339.868554
Iteration   3: objective = -1131.944070
Iteration   4: objective = -1127.300715
Iteration   5: objective = -1126.500899
Iteration   6: objective = -1126.353573
Iteration   7: objective = -1126.322354
Iteration   8: objective = -1126.311858
Iteration   9: objective = -1126.304847
Iteration  10: objective = -1126.298135
Iteration  11: objective = -1126.291099
Iteration  12: objective = -1126.283589
Iteration  13: objective = -1126.275541
Iteration  14: objective = -1126.266904
Iteration  15: objective = -1126.257620
Iteration  16: objective = -1126.247614
Iteration  17: objective = -1126.236773
Iteration  18: objective = -1126.224914
Iteration  19: objective = -1126.211705
Iteration  20: objective = -1126.196528
Iteration  21: objective = -1126.178183
Iteration  22: objective = -1126.154325
Iteration  23: objective = -1126.120390
Iteration  24: objective = -1126.067727
Iteration  25: objective = -1125.980868
Iteration  26: objective = -1125.835227
Iteration  27: objective = -1125.599663
Iteration  28: objective = -1125.249589
Iteration  29: objective = -1124.785039
Iteration  30: objective = -1124.233244
Iteration  31: objective = -1123.631010
Iteration  32: objective = -1123.007474
Iteration  33: objective = -1122.379173
Iteration  34: objective = -1121.752901
Iteration  35: objective = -1121.129623
Iteration  36: objective = -1120.506330
Iteration  37: objective = -1119.875343
Iteration  38: objective = -1119.221726
Iteration  39: objective = -1118.519319
Iteration  40: objective = -1117.724714
Iteration  41: objective = -1116.766372
Iteration  42: objective = -1115.523260
Iteration  43: objective = -1113.783998
Iteration  44: objective = -1111.179801
Iteration  45: objective = -1107.124552
Iteration  46: objective = -1100.932573
Iteration  47: objective = -1092.321644
Iteration  48: objective = -1081.897749
Iteration  49: objective = -1071.461173
Iteration  50: objective = -1063.729364
Iteration  51: objective = -1060.288339
Iteration  52: objective = -1059.433398
Iteration  53: objective = -1059.246114
Iteration  54: objective = -1059.178104
Iteration  55: objective = -1059.132736
Iteration  56: objective = -1059.092704
Iteration  57: objective = -1059.054142
Iteration  58: objective = -1059.015948
Iteration  59: objective = -1058.977764
Iteration  60: objective = -1058.939493
Iteration  61: objective = -1058.901144
Iteration  62: objective = -1058.862776
Iteration  63: objective = -1058.824473
Iteration  64: objective = -1058.786332
Iteration  65: objective = -1058.748453
Iteration  66: objective = -1058.710941
Iteration  67: objective = -1058.673898
Iteration  68: objective = -1058.637426
Iteration  69: objective = -1058.601623
Iteration  70: objective = -1058.566583
Iteration  71: objective = -1058.532391
Iteration  72: objective = -1058.499129
Iteration  73: objective = -1058.466869
Iteration  74: objective = -1058.435672
Iteration  75: objective = -1058.405593
Iteration  76: objective = -1058.376675
Iteration  77: objective = -1058.348952
Iteration  78: objective = -1058.322449
Iteration  79: objective = -1058.297180
Iteration  80: objective = -1058.273150
Iteration  81: objective = -1058.250355
Iteration  82: objective = -1058.228785
Iteration  83: objective = -1058.208421
Iteration  84: objective = -1058.189237
Iteration  85: objective = -1058.171204
Iteration  86: objective = -1058.154286
Iteration  87: objective = -1058.138445
Iteration  88: objective = -1058.123638
Iteration  89: objective = -1058.109821
Iteration  90: objective = -1058.096948
Iteration  91: objective = -1058.084973
Iteration  92: objective = -1058.073849
Iteration  93: objective = -1058.063527
Iteration  94: objective = -1058.053963
Iteration  95: objective = -1058.045111
Iteration  96: objective = -1058.036925
Iteration  97: objective = -1058.029364
Iteration  98: objective = -1058.022386
Iteration  99: objective = -1058.015951
Iteration 100: objective = -1058.010022
plot(sim$X, col=alpha_colors[sim$z], cex=1,
     pch=19, main="EM Fitted Means with RW2 Prior")
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, result_rw2$params$mu)
# Draw arrows showing sequence
for (k in 1:(nrow(mu_matrix)-1)) {
  arrows(mu_matrix[k,1], mu_matrix[k,2],
         mu_matrix[k+1,1], mu_matrix[k+1,2],
         col="orange", lwd=4, length=0.1)
}
points(mu_matrix, pch=8, cex=1, lwd=1, col="orange")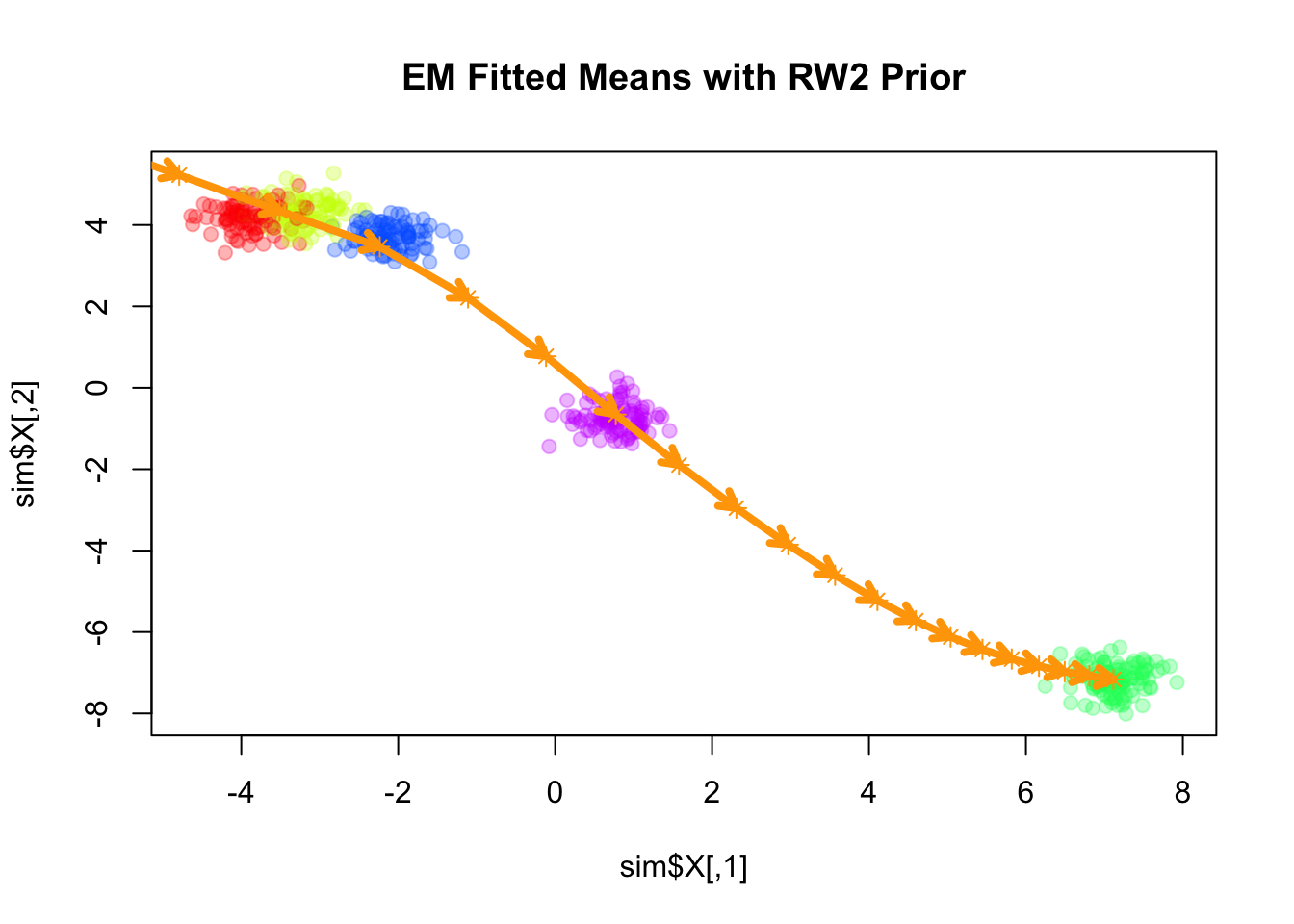

Version Author Date
041218f Ziang Zhang 2025-07-09
028201f Ziang Zhang 2025-07-08

Similar to the RW1 prior, the RW2 prior is also a partially improper prior, as it is invariant to addition of a constant vector as well as a linear trend (in terms of \(k\)) to all component means. As \(\lambda\) increases, the fitted means become closer to a linear trend.

Q_prior_rw2_strong <- make_random_walk_precision(K = 20, d = 2, q=2, lambda=10000)
Q_prior_rw2_strong <- EM_algorithm(
  data = sim$X,
  Q_prior = Q_prior_rw2_strong,
  init_params = init_params,
  max_iter = 100,
  modelName = "EEI",
  tol = 1e-3,
  verbose = TRUE
)
Iteration   1: objective = -3157.728602
Iteration   2: objective = -1106.648394
Iteration   3: objective = -1086.466221
Iteration   4: objective = -1074.714809
Iteration   5: objective = -1067.389971
Iteration   6: objective = -1062.264452
Iteration   7: objective = -1058.282529
Iteration   8: objective = -1055.386219
Iteration   9: objective = -1053.498006
Iteration  10: objective = -1052.333884
Iteration  11: objective = -1051.607395
Iteration  12: objective = -1051.132149
Iteration  13: objective = -1050.803883
Iteration  14: objective = -1050.560226
Iteration  15: objective = -1050.350615
Iteration  16: objective = -1050.108547
Iteration  17: objective = -1049.705044
Iteration  18: objective = -1048.848610
Iteration  19: objective = -1046.892445
Iteration  20: objective = -1042.636367
Iteration  21: objective = -1034.710061
Iteration  22: objective = -1023.171195
Iteration  23: objective = -1010.464150
Iteration  24: objective = -999.721065
Iteration  25: objective = -992.826533
Iteration  26: objective = -989.639211
Iteration  27: objective = -988.680214
Iteration  28: objective = -988.586794
Iteration  29: objective = -988.661556
Converged at iteration 29 with objective -988.661556
plot(sim$X, col=alpha_colors[sim$z], cex=1,
     pch=19, main="EM Fitted Means with RW2 Prior (strong penalty)")
# Turn mu_list into matrix
mu_matrix <- do.call(rbind, Q_prior_rw2_strong$params$mu)
# Draw arrows showing sequence
for (k in 1:(nrow(mu_matrix)-1)) {
  arrows(mu_matrix[k,1], mu_matrix[k,2],
         mu_matrix[k+1,1], mu_matrix[k+1,2],
         col="orange", lwd=4, length=0.1)
}
points(mu_matrix, pch=8, cex=1, lwd=1, col="orange")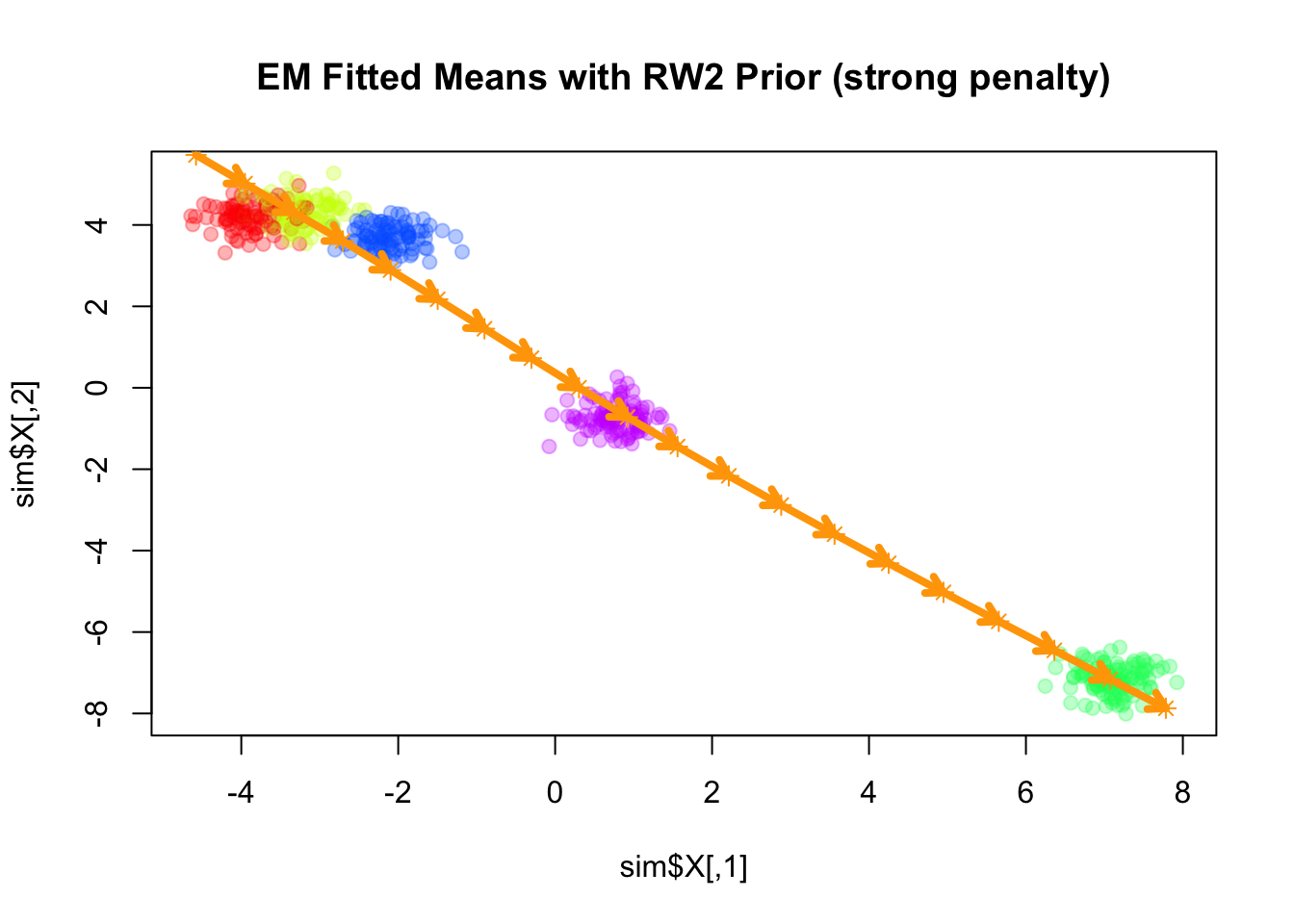

Version Author Date
041218f Ziang Zhang 2025-07-09
028201f Ziang Zhang 2025-07-08 

sessionInfo()
R version 4.3.1 (2023-06-16)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.7.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/Chicago
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] Matrix_1.6-4      matrixStats_1.4.1 mclust_6.1.1      mvtnorm_1.3-1    
[5] MASS_7.3-60       workflowr_1.7.1  

loaded via a namespace (and not attached):
 [1] jsonlite_2.0.0    compiler_4.3.1    promises_1.3.3    Rcpp_1.0.14      
 [5] stringr_1.5.1     git2r_0.33.0      callr_3.7.6       later_1.4.2      
 [9] jquerylib_0.1.4   yaml_2.3.10       fastmap_1.2.0     lattice_0.22-6   
[13] R6_2.6.1          knitr_1.50        tibble_3.2.1      rprojroot_2.0.4  
[17] bslib_0.9.0       pillar_1.10.2     rlang_1.1.6       cachem_1.1.0     
[21] stringi_1.8.7     httpuv_1.6.16     xfun_0.52         getPass_0.2-4    
[25] fs_1.6.6          sass_0.4.10       cli_3.6.5         magrittr_2.0.3   
[29] ps_1.9.1          grid_4.3.1        digest_0.6.37     processx_3.8.6   
[33] rstudioapi_0.16.0 lifecycle_1.0.4   vctrs_0.6.5       evaluate_1.0.3   
[37] glue_1.8.0        whisker_0.4.1     rmarkdown_2.28    httr_1.4.7       
[41] tools_4.3.1       pkgconfig_2.0.3   htmltools_0.5.8.1